SPSS’TE POST-HOC TESTLERİ NE ZAMAN, NASIL KULLANILMALIDIR?
- yöntem istatistik

- 21 Eki 2021
- 3 dakikada okunur
Güncelleme tarihi: 22 Eki 2021
İki gruptan daha çok grup olması halinde, gruplar arası farkın belirlenmesinde kullanılacak istatsitiki yöntem varyans analizidir. Spss’te ANOVA (Analaysis of Variance) Test istatistiği olarak bulunan test analizini yapabilmek için bazı varsayımların sağlanıyor olması gerekmektedir.
Bu varsayımlar;
· Verilerin normal dağılması,
· Homajen olması,
· Toplanabilir olması gerekmektedir.
ANOVA Testi ile gruplar arasında fark olup olmaması tespit edilebilirken farkın hangi gruplardan kaynaklandığı analiz sonucunda bilinmemektedir.
İncelenilen gruplar arasında farkın olması halinde, bu farklılığın tam olarak hangi grupta olduğunu anlamak için post-hoc testleri uygulanmalıdır. Farklılığın hangi gruptan kaynaklandığını test etmek amacıyla hangi post-hoc testinin uygulanacağını seçmek için bir takım varsayımlara bakılır. Spss üzerinden yapılacak olan post-hoc analizinde en önemli unsurlardan biri varyansların eşit dağılıp dağılmamasına göre testin belirlenmesidir.
Eşit varyansta uygulanacak olan post-hoc istatistikler iki metodla incelenir.
Çoklu Karşılaştırma Testleri: Oluşturulan bir matris üzerinden her grubu diğer gruplarla bir bir kıyaslayarak farklı olanları tespit eder.
Çoklu Aralık Testleri: Homojen grup ortalamaları oluşturarak alt kümeler meydana getirerek, farklı olan grubu bulmaya çalışmaktadır.
Spss’te ANOVA testi yapılırken, fark varsa araştırılan grupların hangisinden kaynaklandığını bulabilmek için uygulacak post-hoc testinin seçiminde ilk kriter varyansların eşit olup olmama durumlarıdır. Aşağıda kısaca eşit varyanslı olması veya eşit varyanslı olmaması durumunda kullanılacak post-hoc testlerine yer verilmiş ve kısaca bahsedilmiştir.
Eşit Varyanslı Durumlarda Kullanılabilecek Post-Hoc Testleri
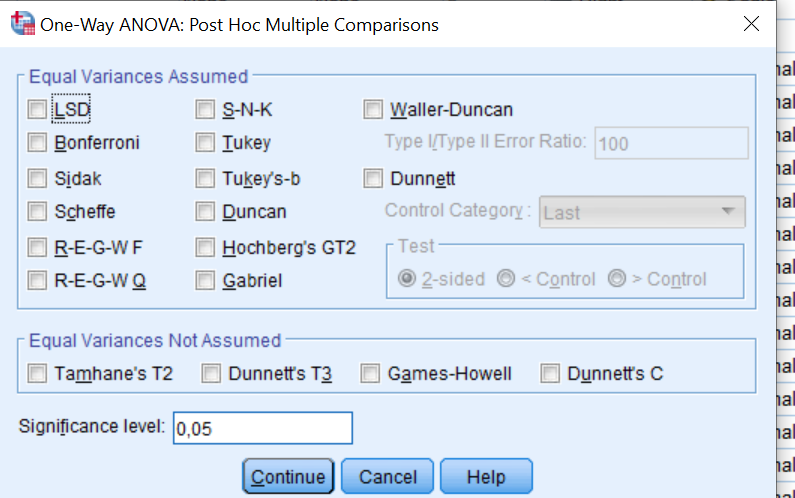
Spss Post-hoc test segmesinde yer alan eşit varyanslı olması halinde kullanılacak post-hoc testleri:
LSD (Least Significant Difference), Bonferroni, Sidak, Scheffe, R-E-G-W F, R-E-G-W Q, S-N-K, Tukey, Tukey’s-b, Duncan, Hochbergs’s GT2, Gabriel, Waller-Duncan, Dunnet
LSD (Least Significant Difference)
Uygulama yapılacak grup sayısının 3’ten çok olması halinde hata verecek bir test istatistiğidir. I.tip hataya karşı korumasız bir özelliktedir. I. tip hata düzeyi α=0,05 seçilmesi halinde grup sayısındaki artışla birlikte her bir grup başına düşen hata da artmaktadır. Bu sebeple aralarındaki farklar ölçülmeye çalışılan grup sayılarının artması halinde önerilen bir istatistik değildir.
Sidak, Bonferronni
Sidak, özellikle LSD testinde varolan I. tip hatayı ortadan kaldırmak için geliştirilmiştir. Hata sayısına sınırlamalar getirebilmektedir. Örneklem büyüklüğünün eşit olması şartı aranmaz.
Bonferronni, eşit örneklem büyüklüğü şartı gerektirmektedir. T testi istatistiği üzerine kurulu olan çoklu karşılaştırma testleri içerisinde yaygın olarak tercih edilen bir metoddur.
Tukey
Çok tercih edilen, güçlü bir çoklu test istatistiğidir. Eşit örneklem şartı gerektirmez.
S-N-K, R-E-G-W F, R-E-G-W Q ve Duncan
Bu metodlar sıralı testleri içermektedir. S-N-K, gruplar için eşit dağılmış alt kümeler meydana getiren ve örneklem sayısının harmonik ortalamasını (gözlem sonuçlarının tersinin aritmetik ortalamaları) dikkate alan bir çoklu test istatistiğidir. Eşit örneklem sayısının olmadığı durumlarda I. tip hata garantiye alanamamaktadır.
Duncan, S-N-K ya benzer yönleri vardır ancak kendine özgü bir tablo kullanmaktadır. Duncan’ın S-N-K test istatistiğine göre daha güvenilir sonuçlar verdiği ileri sürülmektedir. Duncan’ın daha tutarlı olmasında örneklem sayısını dikkate alarak bir α değeri üretmesi vardır. S-N-K’da α 0,05 veya 0,01 olarak kabul edilir. Ancak Duncan da bu değer örneklem sayısına bağlı olarak 0,02, 0,04 gibi değerler de alabilmektedir. Benzer şekilde çoklu aralık testi olan R-E-G-W-F ve R-EG-W-Q test istatistikleri nden R-E-Q-W-Q istatistiği, tıpkı Duncan post-hoc test istatistiğinde olduğu gibi α anlamlılık düzeyini grup sayısı dikkate alınarak esnek olmasını sağlayabilmektedir.
Tukey’s B
Tukey’s B, S-N-K’ ya benzer bir mantıkla uygulanan ve eşit olmayan örneklem sayılarının olduğu hallerde I. tip hatayı tolere edemeyen bir post-hoc test istatistiğidir.
Scheffe
Farklılığın tespit edilmesi için uygulama yapılacak gruplar arasındaki doğrusal kombinasyonların karşılaştırılmasıamacıyla geliştirilen bir yöntem olan Scheffe; en esnek, çok fazla grup olması halinde hata miktarını kontrol edebilen ve eşit gözlem sayısı şartı olmayan bir metoddur.
Hochberg'in GT2'si, Gabriel
Hochberg’s GT2 istatistiği, Tukey’e benzemekle birlikte Studentized maximum modulus (genişletişmiş t modülü) ile çalışan bir yöntemdir. Aynı şekilde Gabriel istatistiği de genişletilmiş t modülü ile gerçekleştirilir ancak eşit örneklem sayısı şartı gerektirmez. İki testin de Tukey kadar güçlü olmadığı kabul edilir.
Waller-Duncan
Bayesian yaklaşım gösteren Waller-Duncan post-hoc test istatistiği, örneklem sayılarının eşit olmadığı durumlarda grup sayılarının harmonik değerini kullanmayı öneren post-hoc testidir.
Dunnett
Yanlızca bir grubun birden fazla grupla kıyaslanmasının gerektiği durumlarda bu çoklu test istatistiğinin kullanılması önerilmektedir.
Eşit Varyans Olmayan Durumlarda Kullanılabilecek Post-Hoc Testleri
Eşit varyans olmaması durumunda kullanılabilecek çoklu test istatistik metodları; Games-Howell Test İstatistiği, Tamhane’s T2 Test İstatistiği, Tamhane’s T3 Test İstatistiği, Dunnet’s C Test İstatistiği ve Dunnet’s T3 Test İstatistiği’dir. Tamamı “çoklu aralık testi” grubunda yer almaktadır. Bu türlerde farklılık “student t” veya “genişletilmiş t modülüne” göre belirlenmektedir. Games-Horwell post-hoc test istatistiği iki grupta da çalışabilmektedir. Tamhane’s T2 ve Tamhane’s T3 metodları yalnızca “student t” ile çalışır ve güçlüdürler. Dunnet’s C ve Dunnet’s T3 test istatistikleri ise yalnızca genişletilmiş t modülü tabanında çalışmaktadır.
Konunun daha net anlaşılması için aşağıda Çizelge 1 ve Çizelge 2’de post-hoc testlerinin genel kullanılabilme durumları gösterilmektedir.
ANOVA Testi yapıldıktan sonra varyansın eşit olup olmama durumuna göre seçilen Post-hoc test istatistiği ile farklılığın kaynaklandığı gruplar bulunur ve araştırma raporunda bu bilgiye yer verilir.




Yorumlar