Yapısal Eşitlik Modeli
- yöntem istatistik

- 20 Tem 2021
- 3 dakikada okunur
Güncelleme tarihi: 22 Eki 2021
Bilimsel araştırmalar birçok farklı alanda yapılmaktadır. Araştırmalarda değişkenler arasındaki nedensel ilişkiye veya korelasyon ilişkisine dayanarak araştırmaya ait teoriler ortaya konulur. Bu teorilerin doğruluğu için kullanılan hipotezler için birçok farklı yöntem kullanılır. Bu yöntemlerden biri ise yapısal eşitlik modelidir.
Yapısal eşitlik modeli özellikle sosyal çalışmalar, psikolojik çalışmalar veya pazarlama gibi alanlarda kullanılan istatistik yöntemdir. Yapısal Eşitlik Modellemesi (Structural Equation Modeling) kısaltması YEM'dir.
YEM için tarihsel sürece bakarsak ilk olarak sosyoloji bilimi için 1977 yılında kullanılmıştır.1980'li yıllarda akademik birçok çalışmalarda kullanılmıştır. Bu yöntem günümüzdeki haline gelirken birçok aşamadan geçmiştir.
1896 yılında Karl Pearson, korelasyon katsayısının formülünü bulmuştur. Daha sonra en küçük kareler yöntemi de geliştirilmiş bunlarla doğrusal regresyon modeli oluşturulmuştur.
Speraman ise 1904 yılında korelasyon katsayısı formülünü geliştirerek doğrulayıcı faktör analizinin temelini ortaya çıkarmıştır.1940’lı yıllarda ise doğrulayıcı faktör analizi istatistiksel bir araç olarak kullanılmaya başlanmıştır. 20.yüzyılın başında ise Wright, Path analizini geliştirmiştir. Path analizinin diğer adı yol analizidir. 20.yüzyılın ikinci yarısında doğrulayıcı faktör analizinin çalışmalarına başlanmış 1960 yılında Karl Joreskog tarafından tamamlanmıştır.1969 yılında kullanılmaya başlanmıştır.
Ortaya çıkan tüm analizler sonucunda gizli değişken kavramı ortaya çıkmıştır. Bu kavram ise yapısal eşitlik modelinin temelini oluşturmuştur. Araştırmacıların YEM analizini birden çok nedenden kullanmak isterler. Bunlardan bazısı;
Bilimsel bazı araştırmaların daha net ve ayrıntılı açıklanması için gözlemlenen değişkenlerin birden çok seçilmesi öngörülür. YEM analizi diğer analizlere göre daha ayrıntılı ve kapsamlı olduğu için araştırmacılar bu analizi daha çok kullanmak isterler.
Ayrıca her istatistiki çalışmada ortaya çıkabilen ölçüm hataları vardır. Bu hata diğer analizlerde yok sayılırken YEM analizinde hesaplanır bu da bu analizin daha güvenliği olduğu gösterir.
Bir diğer neden ise, YEM analizinin durağan olmamasıdır. YEM analizi sürekli kendini geliştirir ve bu yüzdende her yeni, farklı teorik modellerin analizlerinde kullanılır. YEM'de gizli değişken (latent variable) ve gözlenen değişkenler (observed variable) kullanılır ve bu yöntem bu değişkenler arasındaki ilişikiyi belirler bu değişkenlere ait teorilere dayalı hipotezlerin doğru olup olmadıklarını test eder.
YEM modellerine ilk olarak araştırılmak istenen değişkenler nelerdir, bunların arasında ilişki var mıdır bu soruları sorularak başlanılır. Bu soruların ana cevap kaynakları ise bilimsel bir olgu olmalıdır. Böylece YEM analizi için model belirlenmiş olur.
Model belirlendikten sonra ise modelin parametrelerine ilişkin varyans ve kovaryans değerlerine bakılır. Bu değerlere göre modelin tanımlanma durumu tespit edilir.
Tanımlanma durumu tespit edilen modelde tahmin işlemleri uygulanır. Tahmin işlemleri için gözlenen değişkenlere ve modelin parametrelerine bakılır. Tahmin işlemlerini yapıldıktan sonra modelin uyumuna bakılır. En son işlemde ise modelde anlamlı olmayan değişkenler çıkarılır veya modele uyumlu ilişkiler eklenir.
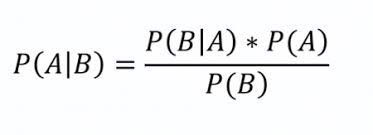
YEM analizi 2 temel yaklaşıma ayrılır:
1.Kompetant Tabanlı: Bu yaklaşımın diğer ismi en küçük kareler tabanlı yaklaşımdır. Bu yaklaşımda veriler normal dağılıma sahip olmalıdır. Küçük örnekler için kullanılır. Varyans ve t değerleri bu modelde belirlenir. Bu yaklaşımda ya gizli değişkenler arasındaki ilişkiler incelenir ya da gizli değişkenler ile gözlenen değişkenler arasındaki ilişki incelenir. Her iki durum içinde en uygun yaklaşımdır. Yaklaşımın amacı yokluk hipotezinin anlamlı olduğunu ispat etmektir.
2.Kovaryans Tabanlı: Bu yaklaşımın diğer ismi en büyük olabilirlik yaklaşımıdır. Bu yaklaşımda veriler normal dağılıma sahip olmak zorunda değildir. Büyük örnekler için kullanılır. Bu yaklaşımın amacı yokluk hipotezinin anlamsız olduğunu tespit etmek için kullanılır. Bu yaklaşım kovaryans yapısıyla en iyi kovaryans yapısı arasındaki ilişkiyi inceler.
BAYES TEOREMİ Bayes teoremi bayes yapısal eşitlik modelinin temelini oluşturur. Bir olayın olma olasılığı ile gerçekte olma olasılığını arasındaki ilişkiyi gösterir. Bayes Teoremi formülü;
BAYES YAPISAL EŞİTLİK MODELİ Bayes yapısal eşitlik modeli yapısal eşitlik modeli yerine kullanılan yeni bir modeldir. Bayes yapısal eşitlik modelinin kısaltması BYEM’dir. BYEM sağlık, psikolojik, sosyal alanlarda kullanılabilir. Kullanım alanı YEM’de olduğu gibi oldukça fazladır. BYEM analizinin en önemli özelliği ön bilginin var olmasıdır. Ön bilgi model parametrelerin doğru ve yeterli olduğunu gösterir. Modelin nasıl dağıldığı, ölçeğin ne olduğu gibi soruların cevapları ön bilginin alanına girer.
BYEM analizinde yakınsama Gelman-Rubin yakınsaması ile yapılır. Yine bu analizin uyumu için p değerine bakılır. P değeri 0.3-0.7 arasında ise modelin uyumlu olduğu p değeri 0 ise modelin uyumsuz olduğunu söyleyebiliriz.
BYEM doğrusal olmayan, normal dağılmayan, karışık kategorik değişenlerle kullanılabilir. Ayrıca yine kayıp verilerin varlığı da bu analizin kullanılmasını engellemez. BYEM analizi Markov Zinciri Manto Carlo istatistiklerine dayanır. BYEM analizi çok küçük örneklemler için kullanılabilir.
BYEM analizinde önsel bilgiler kullanıldığı için modellerde hatalar minimum seviyededir yani modeller iyi model olarak adlandırılır. BYEM analizini AMOS ve WinBUGS yazılımları yapmaktadır.
REGRESYON ANALİZİ Regresyon analizi değişkenler arasındaki ilişkiyi modelleyen ve inceleyen bir yöntemdir. Yani bağımlı değişkenler ile bağımsız değişkenler arasındaki ilişkiyi inceler. Ancak bu durum yapısal eşitlik modeli ile kıyasladığımızda regresyon analizinin yetersizliğini gösterir. Çünkü analize alınan bağımsız değişkenler arasındaki ilişki incelenmek istendiğinde regresyon analizi cevap veremez ekstradan ölçekler, işlemler yaparak bunun cevabı verilebilir.
Oysa yapısal eşitlik modelinde kullanılan analiz yöntemleri sürekli gelişen, ilerleyen oldukları için bağımsız değişkenler arasındaki ilişkiyi de kısa sürede verecektir. Regresyon analizi birden fazla değişkenler için de kullanılır. Ancak yapısal eşitlik modeli analizi bu değişkenler için de daha pratiktir. Ayrıca modelde var olan gizli değişkenler regresyon analizinde yok sayılırken yapısal eşitlik modelinde mutlaka bu değişkenler hesaplanır ve analiz edilir.

Yorumlar